A generalization of Coleman's
p-adic integration theory
(New version 20.4.97, still preliminary)

Amnon Besser
(E-mail, publications)

Coleman.ps.gz (104k, unpack using gunzip)

Abstract

What we do here is to define a generalization of Coleman's p-adic integral (``Torsion points on curves and p-adic abelian integrals'' in Annals of Math. 121, p. 111-168) for odd order de Rham classes on a smooth projective algebraic variety X over a p-adic field K with good reduction V. It turns out that this theory allows one to associate to each class $[\omega ]\in F^{j+1}H_{dR}^{2j+1}(X/K)$ a functional on the collection of j dimensional smooth subvarieties of X having good reduction
Y\rightarrow \int_Y[\omega ]
with degrees of freedom given such that the combination
\sum n_i\int_{Y_i}[\omega ]
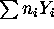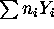is uniquely defined whenever \sum n_iY_i is a cycle homologically equivalent to 0. We also prove a theorem which states that this last expression can be computed alternatively by interpreting the p-adic Abel-Jacobi image of the cycle \sum n_iY_i as a functional on 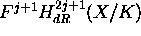F^{j+1}H_{dR}^{2j+1}(X/K) and evaluating it on [\omega ]. This is verified first in the case j=0. The construction of the integral is performed using two different methods. One is an extension of the method of Coleman. The other is using a new cohomology theory, called the finite polynomial cohomology, which is related to the finite cohomology of Niziol. The basic properties of this cohomology theory which we prove turn out to be sufficient for proving the connection with the Abel-Jacobi map.